My Take on Einstein’s General Relativity and Spacetime
Hey everyone! I’m Jason Pandian, CEO and Founder of Astron Dynamics. While exploring the concept of spacetime through General Relativity (GR), I realized that time is a fundamental and measurable aspect of all cosmic events. Without time, we can’t measure change, and without observing space, time itself has no context—it’s through the fabric of spacetime that we define and understand both.
The Concept of the Time Dilation Diagram
In general relativity, space behaves like a 4-dimensional fabric that stretches and bends due to the mass and energy within it—similar to how pizza dough bends and stretches when you place objects inside it. I started by imagining how mass and energy cause this bending and then connected it to time dilation, where gravity affects the passage of time at different altitudes.
I started with a simple 2D clock near Earth’s surface and visualized how time would scale as you move farther from Earth, much like geometric scaling. What amazed me is that while time is a universal unit, it’s not equal for all events in the larger astronomical picture. Time scales differently not just from the observer’s point of view, but also for others who are in different parts of these events (based on distance, mass, and energy)—and it’s true. This means that the time we observe in one region of space could be different in another, but both are part of the same larger astronomical picture.
Time as an Object in space!
I imagined time as an object in space under geometric scaling, and this made sense to me. Using GR, I calculated how this “time object” changes at different altitudes (x-axis) around Earth on the y-axis. Since I was imagining time as an object, I needed a scaling reference, so I plotted both y-axes to show time. The experienced time (output) is divided by 2 to maintain the scaling on both y-axes—hey, no negative time actually, just for visualization!
Now, with the time dilation diagram, you become the observer of a particular point and see how time scales for your observing event. That’s the essence of the time dilation diagram. For example, at your observer point, time might be 0.99, while for a nearby observer, it could be around 1.00. Isn’t it amazing to see how time difference in different places in space?
Proof of Concept
To explore the time dilation diagram further, I developed a Python script that visualizes how time scales at different altitudes near a celestial body like Earth. Using astropy constants for Earth’s mass and radius, I calculated how time behaves due to gravitational effects.
import numpy as np
import plotly.graph_objects as go
from astropy.constants import G, c, M_sun, R_sun, M_earth, R_earth # Importing constants from astropy
from typing import Union
def time_dilation(r: np.ndarray, G: float, M: float, c: float) -> np.ndarray:
"""Calculate the time dilation factor near a celestial body."""
if np.any(r <= 2 * G * M / c**2):
raise ValueError("Distance must be greater than the Schwarzschild radius.")
return np.sqrt(1 - (2 * G * M) / (r * c**2))
def experienced_time(dilation_factor: np.ndarray, time_at_infinity: float) -> np.ndarray:
"""Calculate the experienced time given the time dilation factor."""
return time_at_infinity * dilation_factor
def plot_time_dilation(
altitude_start: float,
altitude_end: float,
num_points: int,
mass: float,
radius: float,
G: float,
c: float
) -> None:
"""Plot the time dilation experienced near a celestial body, showing total time across both positive and negative y-axes."""
# Generate distances from the surface
altitude_values: np.ndarray = np.linspace(altitude_start, altitude_end, num_points) # Altitudes in meters
r_values: np.ndarray = radius + altitude_values # Distance from the center of the body
# Calculate time dilation factor at each distance
time_dilations: np.ndarray = time_dilation(r_values, G, mass, c)
# Assume 1 second at infinity
time_at_infinity: float = 1 # 1 second at infinity
# Calculate experienced time at each distance
experienced_times: np.ndarray = experienced_time(time_dilations, time_at_infinity)
# Convert experienced times to nanoseconds
experienced_times_nanoseconds: np.ndarray = experienced_times * 1e9 # Convert seconds to nanoseconds
# Shift to start the y-values from 0
experienced_times_shifted: np.ndarray = experienced_times_nanoseconds - experienced_times_nanoseconds[0]
# Create Plotly figure
fig: go.Figure = go.Figure()
# Plot positive half of the total experienced time
fig.add_trace(go.Scatter(
x=altitude_values / 1e3, # Altitude in kilometers
y=experienced_times_shifted / 2, # Positive Half of Shifted Experienced Time (ns)
mode='lines',
line=dict(color='black', width=2),
name="Positive Half of Total Time",
hovertemplate="Altitude: %{x:.2f} km<br>Total Experienced Time: %{customdata:.2f} ns",
customdata=experienced_times_nanoseconds # Show total time in hover info
))
# Plot negative half of the total experienced time
fig.add_trace(go.Scatter(
x=altitude_values / 1e3, # Altitude in kilometers
y=-experienced_times_shifted / 2, # Negative Half of Shifted Experienced Time (ns)
mode='lines',
line=dict(color='black', width=2),
name="Negative Half of Total Time",
hovertemplate="Altitude: %{x:.2f} km<br>Total Experienced Time: %{customdata:.2f} ns",
customdata=experienced_times_nanoseconds # Show total time in hover info
))
# Customize layout
fig.update_layout(
title="Time Dilation Diagram",
xaxis_title="Altitude Above Body's Surface (km)",
yaxis_title="Half of Total Experienced Time (ns)",
xaxis=dict(showgrid=True, zeroline=True),
yaxis=dict(showgrid=True, zeroline=True),
height=600,
width=800,
legend=dict(x=0.1, y=0.9),
template='plotly_white' # A cleaner background
)
# Add subtitle using annotation
fig.add_annotation(
text="Total Experienced Time Near Celestial Body (Positive + Negative Curves)",
xref="paper", yref="paper",
x=0.5, y=1.05, # position the subtitle above the title
showarrow=False,
font=dict(size=14)
)
# Show the figure
fig.show()
def main() -> None:
"""Main function to execute the time dilation plot."""
try:
plot_time_dilation(0, 3e7, 300, M_earth.value, R_earth.value, G.value, c.value) # Plotting for Earth
except ValueError as e:
print(e)
if __name__ == "__main__":
main()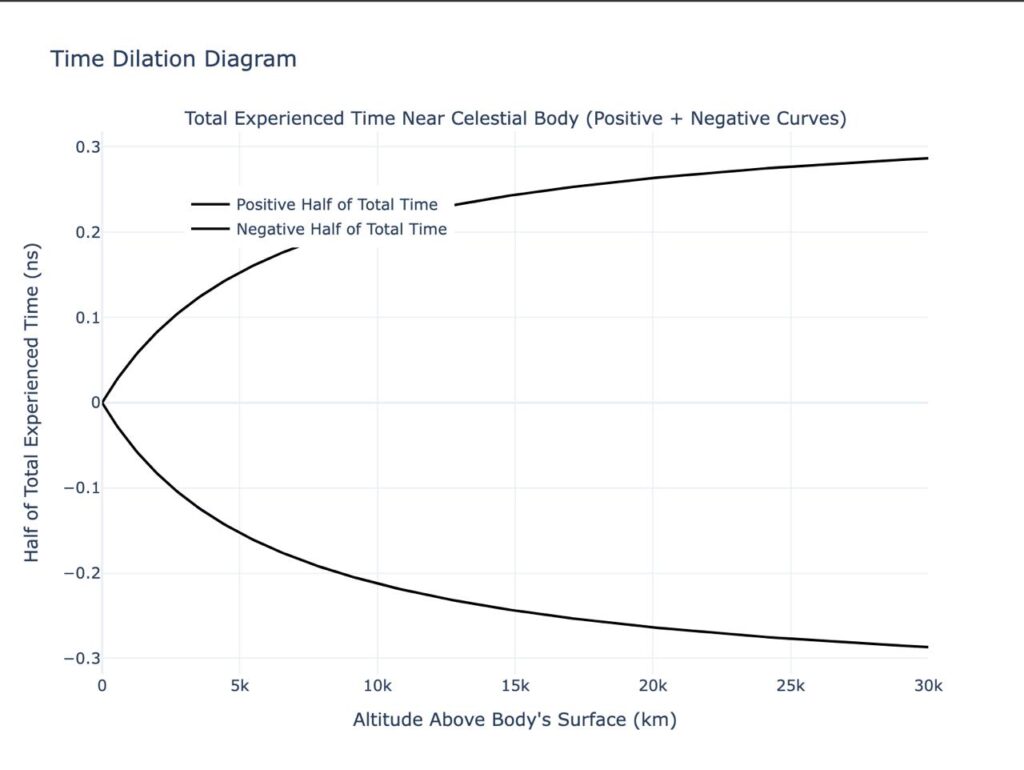
Time Dilation Diagram
What’s Going On Here?
To explore the time dilation diagram further, I developed a Python script that visualizes how time scales at different altitudes near a celestial body like Earth. Using astropy constants for Earth’s mass and radius, I calculated how time behaves due to gravitational effects.
In the next part of the script, I plotted the time dilation graph across altitudes, showing how experienced time changes in nanoseconds as you move away from Earth. I used Plotly to make the diagram, which shows total experienced time divided into positive and negative halves. The result is a symmetrical graph that helps visualize time dilation, giving an intuitive understanding of how gravity affects the passage of time.
For example, when calculating time at different altitudes near Earth, you can see even the smallest differences, down to nanoseconds. The farther you go from Earth, the more time dilates, just as general relativity predicts. What’s interesting is that this graph isn’t just theoretical—it could be practical for space education too.
Beauty of curve
I see the time dilation diagram as a curve that relates to spacetime. When you think of black holes, this diagram would have different wave peaks, and the same goes for the Sun’s time dilation. Time is essential for measuring and observing events in space—it’s what makes spacetime.
Conclusion
In conclusion, think of the time dilation diagram as a simple visual concept that lays the groundwork for understanding how space and time interact in celestial events. This diagram is a tool to visualize spacetime’s complexities and will be expanded later. For now, it captures my thinking on how gravity influences the passage of time in the universe.
